Butter, Cheese and Depth-first search

Tic-Tac-Toe (or as we call it in the Netherlands, “Boter Kaas en Eieren”) is a game you probably have played at least once, and if you did, you most assuredly finished with a draw (leaving you and your opponent equally bored as when you started the darned game). In contrast to games like Chess, the noble sport of Tic-Tac-Toe is simple enough for our feeble minds to plan to its inevitable end:

Why you draw

When you are mentally preparing your moves, your brain is performing an algorithm known to Computer Scientists as Depth-first search.

Depth-first search is an algorithm that works on trees. A tree is a graph that contains a collection of nodes that are connected in a parent-child relationship. Imagine a hereditary tree where one parent can have multiple children (without loops, this family cannot travel through time):

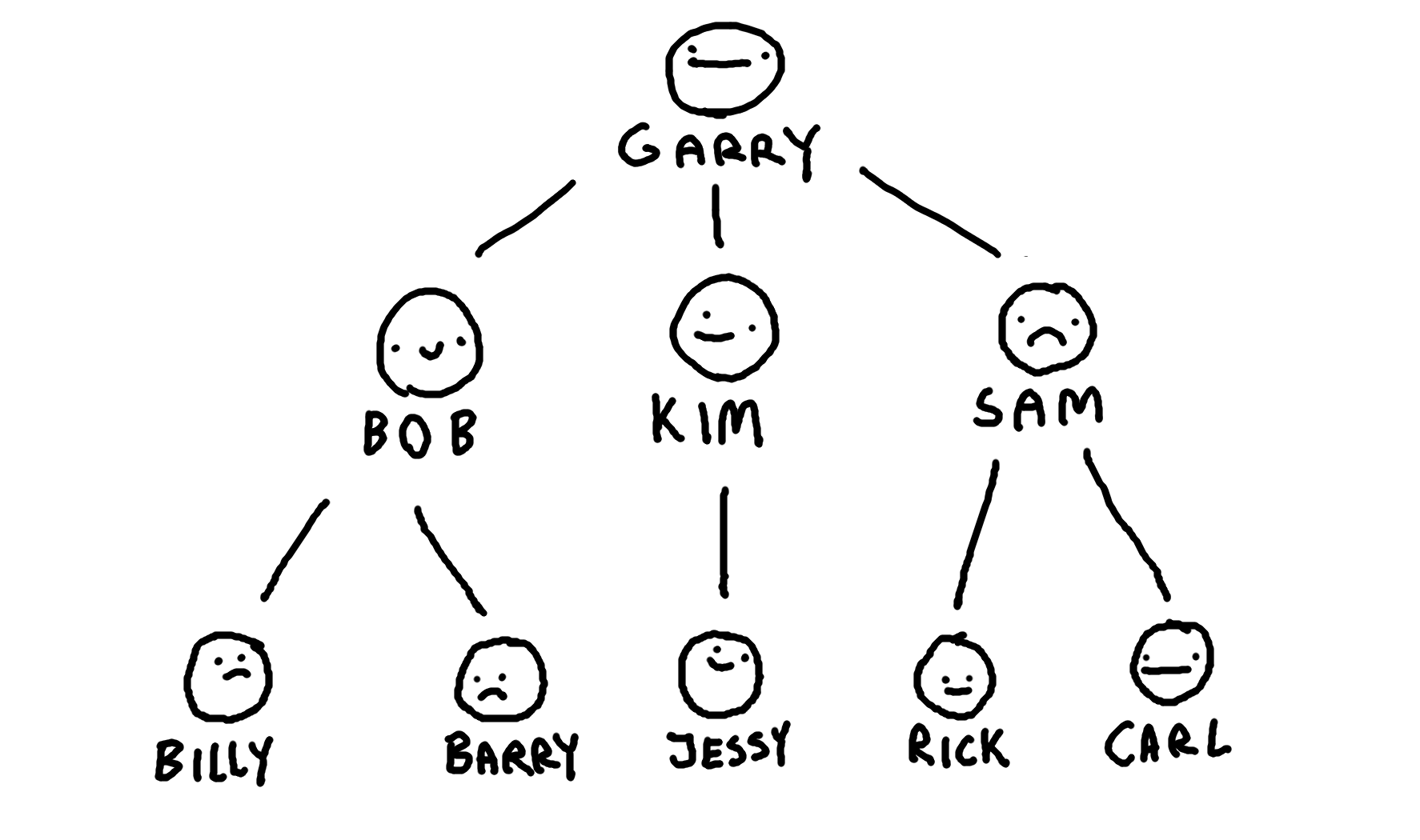
Depth-first search is a searching algorithm that traverses down a branch of the tree and checks for every node in the branch if a particular condition has been met. If it reaches a leaf, it moves back up the tree and starts traversing the next alternative branch. For example, imagine the algorithm looking for Jessy, it would find him like so:

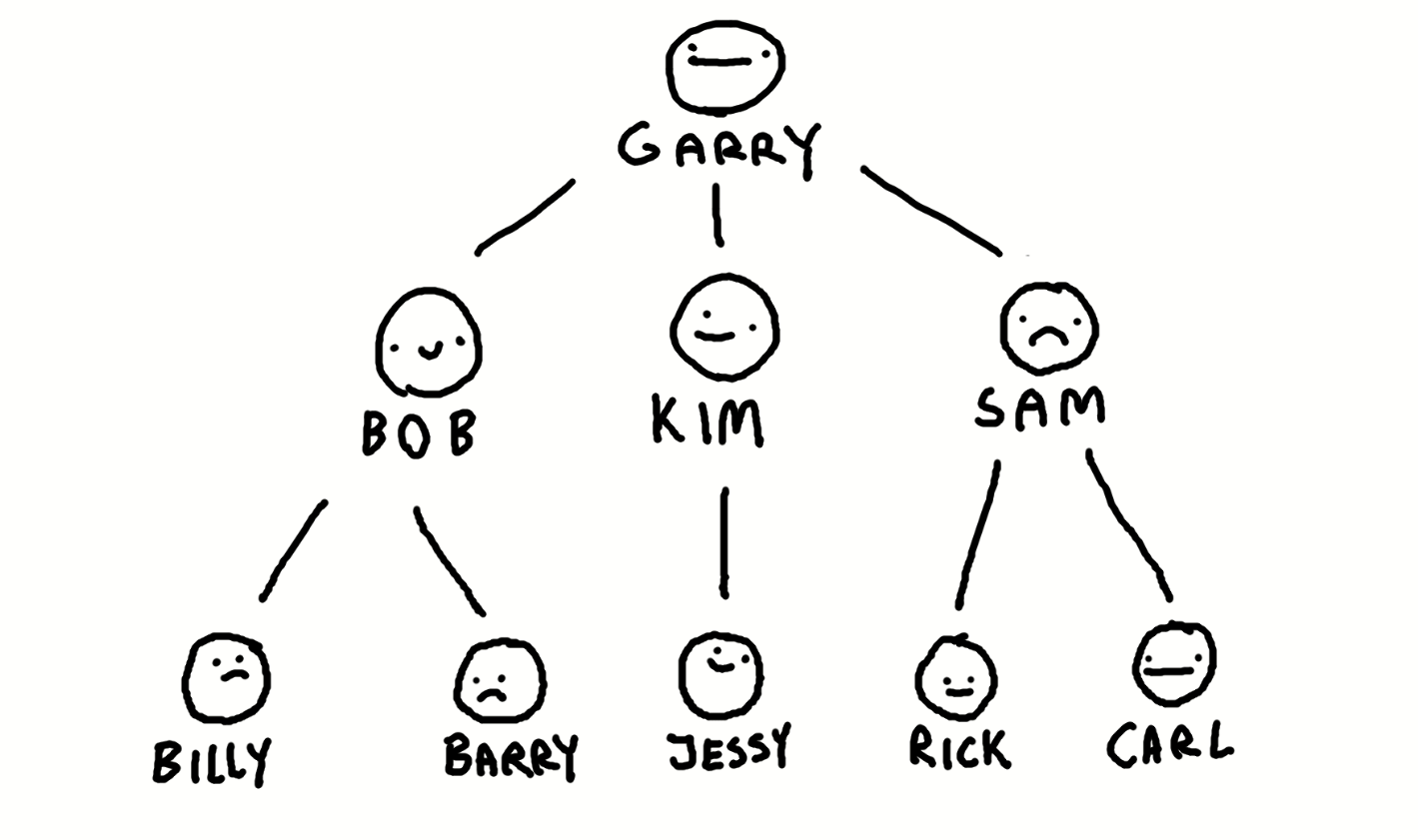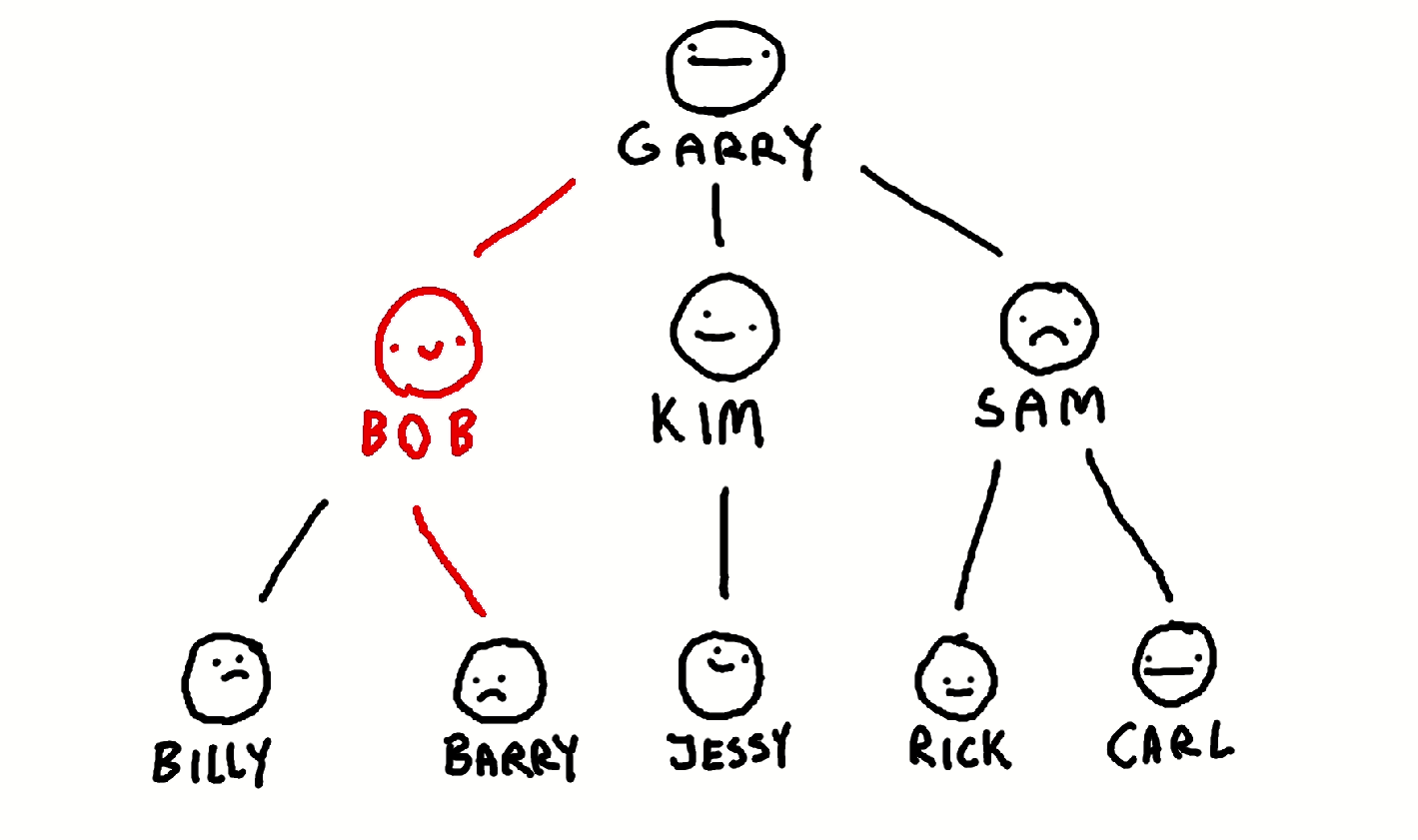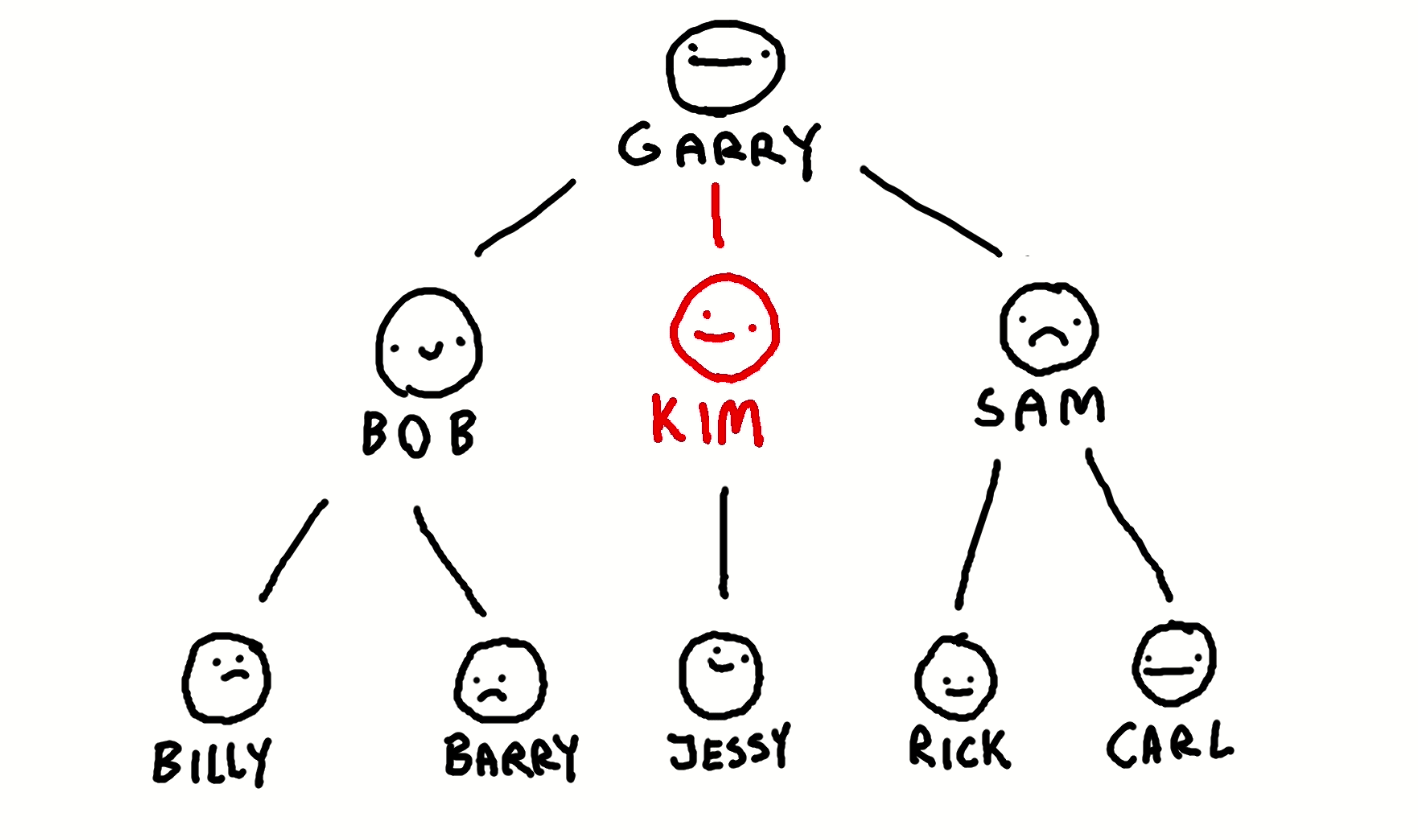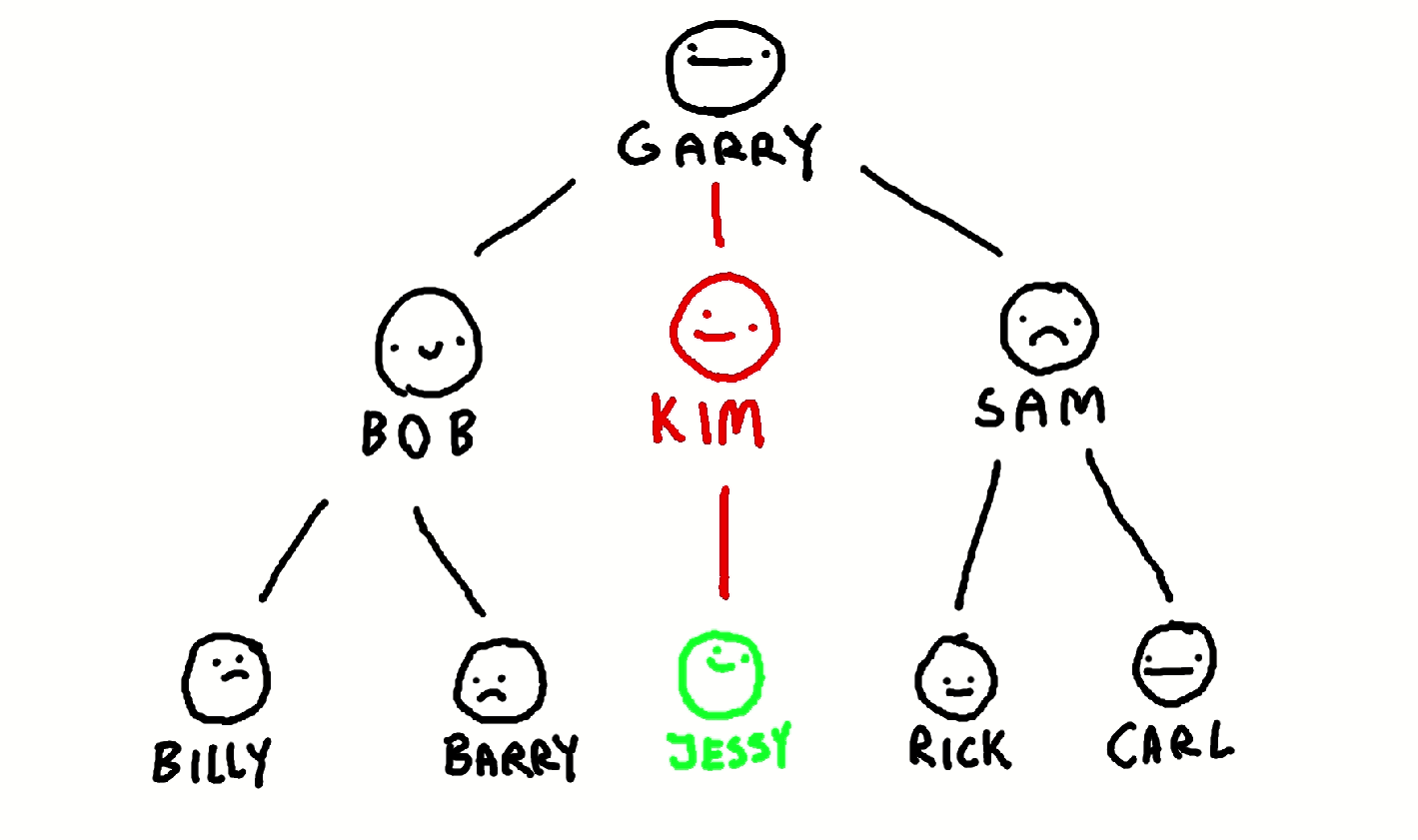
One can see how this simple search can help you solve Tic-Tac-Toe: you mentally imagine what will happen if you place a marker on the board and envision the end-game state that will occur as a result of that choice. If this end-game state does not appeal to you, you imagine another sequence of events that will most likely make you win. Don’t believe me? Try to beat the algorithm yourselves below!

Stepping up the game

In an effort to increase the complexity of this game, bored scientist have invented Meta Tic-Tac-Toe. A game that cannot be trivially solved, and is much more fun to play as a result. In part 2, we will discuss this game and how it can be constructed using recursion.