Butter, Cheese and Recursion

In my previous post, I discussed Tic-Tac-Toe (TTT) and why it’s so easily solved. Today, you will learn about Meta Tic-Tac-Toe (M-TTT), and how its increased complexity can make the game much more fun to play.

The name of the game is the game

The playing field of TTT consist of a 3 by 3 grid of 9 cells in total, and all M-TTT does is insert a new TTT grid in every cell. Thus, M-TTT is a TTT grid where every cell is a TTT grid in itself:

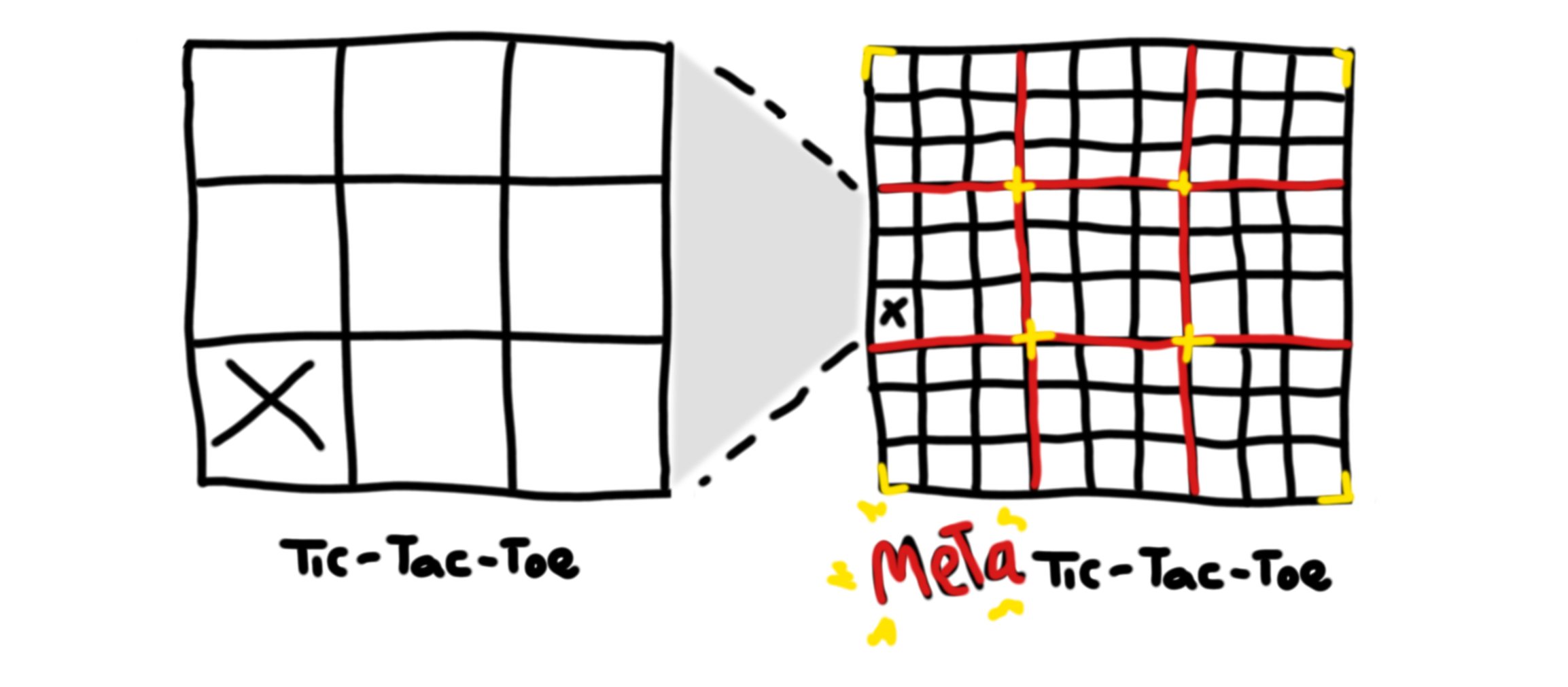
This concept is known to programmers as recursion: defining something by using its own definition. Of course there needs to be a base case to this recursive definition, such that the definition eventually resolves to a meaningful answer. A base case is an alternative definition that is not recursive, and eventually any recursive definition should resolve to that base case. For example, let’s take a look at the following piece of code:

int recursiveMethod(int level)
{
    if (level < 1)
      return 0;
    return 1 + recursiveMethod(level - 1);
}

int result = recursiveMethod(10);

In this little piece of C code, the recursiveMethod adds 1 to the result of recursiveMethod, except when the passed level argument dips below 1 (in other words, less or equal to 0). This if (level < 1) is the base case that prevents the method from recursively adding 1 to its own results until the end of time (or until your call stack decides to overflow).

Similarly in M-TTT, not defining a base case will mean we have an infinite amount of TTT grids nested in TTT grids, and good luck finding somebody to play that game with you. The base case of M-TTT is the number of nested TTT grids that must exist until the cells are simply empty playing fields. Generating our M-TTT grid can thus be achieved like so:

Grid generateMetaGrid(int level)
{
    Grid grid;
    if (level < 1)
      return grid;

    for (int cellIndex = 0; row < grid.size(); cellIndex++)
        grid.setCell(cellIndex, generateMetaGrid(level - 1));

    return grid;
}

Grid metaTTTGrid = generateMetaGrid(1);

The C++ code snippet omits a lot of details, but generally is should bring the point across. When the recursion level is less or equal to 0 we simply return a grid with empty cells, otherwise we fill each cell of the grid with a new recursively defined meta grid, but with one level of recursion less (note the level - 1). The call generateMetaGrid(1) thus generates a meta grid where every cell has another grid stored within, but those nested grids themselves only contain empty cells (as their constructing method was called with a level of 0).

Recursive game-play

A conventional game of M-TTT (our recursive grid of level 1) follows a simple sequence of events:

1. The first player can choose any cell to mark. The location of this cell within its grid is remembered (UpperLeft, UpperMiddle, UpperRight, etc)
2. The following player must mark a cell of a nested grid at the same relative location of the previously marked cell.
3. Go to step 2 until one of the nested grids has a winning sequence of marked cells. This winning grid is marked as such.
4. Go to step 2 until a sequence of nested grids have been marked as ‘won’ by the same player. The player who has won these nested grids has won the game.

Especially step 2 might seem somewhat confusing, so I encourage you to simply scroll down to the section below and simply play the game yourselves. It should become clear what is meant with ‘relative location’ once you see the effects of marking an empty cell.

Now, once you understand the core concepts behind M-TTT, you might begin to see how it will work for any arbitrary number of nested TTT grids. The player must always place their mark in a grid that has the same relative location as the the previously marked cell. Where, with ‘relative location’, we mean the location of the cell relative to its containing grid. Propagating this rule throughout all levels of the nested grid allows us to easily determine the allowed moves:

1. Determine the absolute path of the previously marked cell. For example, in a grid of 2 levels deep, a cell might be marked in the top-left of the center grid at the bottom-right grid of the root grid.
2. Reverse this this absolute path and drop the final relative entry, this is the grid that can be marked. For instance, the example above would indicate that the player can mark the center grid of the top-left of the root grid.

All this might seem a little complex at first sight, but trust me, the game is still trivially simple once you actually start to play it.

Try it!

Of course, this post would not be complete without a neat little demonstration! The interactive window below allows you to generate a TTT game of any Meta level between 0 and 2 ¹. Go find a bored opponent, and play some M-TTT!

Now you know how the game works, the true place for any TTT game to be played is on a piece of paper (or in the dirt, whilst waiting for the hourly bus to arrive). Simply grab a pen, some paper, and then ask your friend: